Graphs
A graph is a non-linear data structure that can be looked at as a collection of vertices (or nodes) potentially connected by line segments named edges.
some common terminology used when working with Graphs:
- Vertex - A vertex, also called a “node”, is a data object that can have zero or more adjacent vertices.
- Edge - An edge is a connection between two nodes.
- Neighbor - The neighbors of a node are its adjacent nodes, i.e., are connected via an edge.
- Degree - The degree of a vertex is the number of edges connected to that vertex.
Directed vs Undirected
- Undirected Graphs
- An Undirected Graph is a graph where each edge is undirected or bi-directional. This means that the undirected graph does not move in any direction.
For example, in the graph below, Node C is connected to Node A, Node E and Node B. There are no “directions” given to point to specific vertices. The connection is bi-directional.
- The undirected graph we are looking at has 6 vertices and 7 undirected edges.
- Vertices/Nodes = {a,b,c,d,e,f}
- Edges = {(a,c),(a,d),(b,c),(b,f),(c,e),(d,e),(e,f)}
- Directed Graphs (Digraph)
- A Directed Graph also called a Digraph is a graph where every edge is directed.
- Unlike an undirected graph, a Digraph has direction. Each node is directed at another node with a specific requirement of what node should be referenced next.
- The directed graph above has six vertices and eight directed edges
- Vertices = {a,b,c,d,e,f}
- Edges = {(a,c),(b,c),(b,f),(c,e),(d,a),(d,e)(e,c)(e,f)}
Complete vs Connected vs Disconnected
-
Complete Graphs A complete graph is when all nodes are connected to all other nodes.
-
Connected A connected graph is graph that has all of vertices/nodes have at least one edge.
-
Disconnected A disconnected graph is a graph where some vertices may not have edges.
Acyclic vs Cyclic
- Acyclic Graph
- An acyclic graph is a directed graph without cycles.
- A cycle is when a node can be traversed through and potentially end up back at itself.
Here is an example of 3 acyclic graphs:
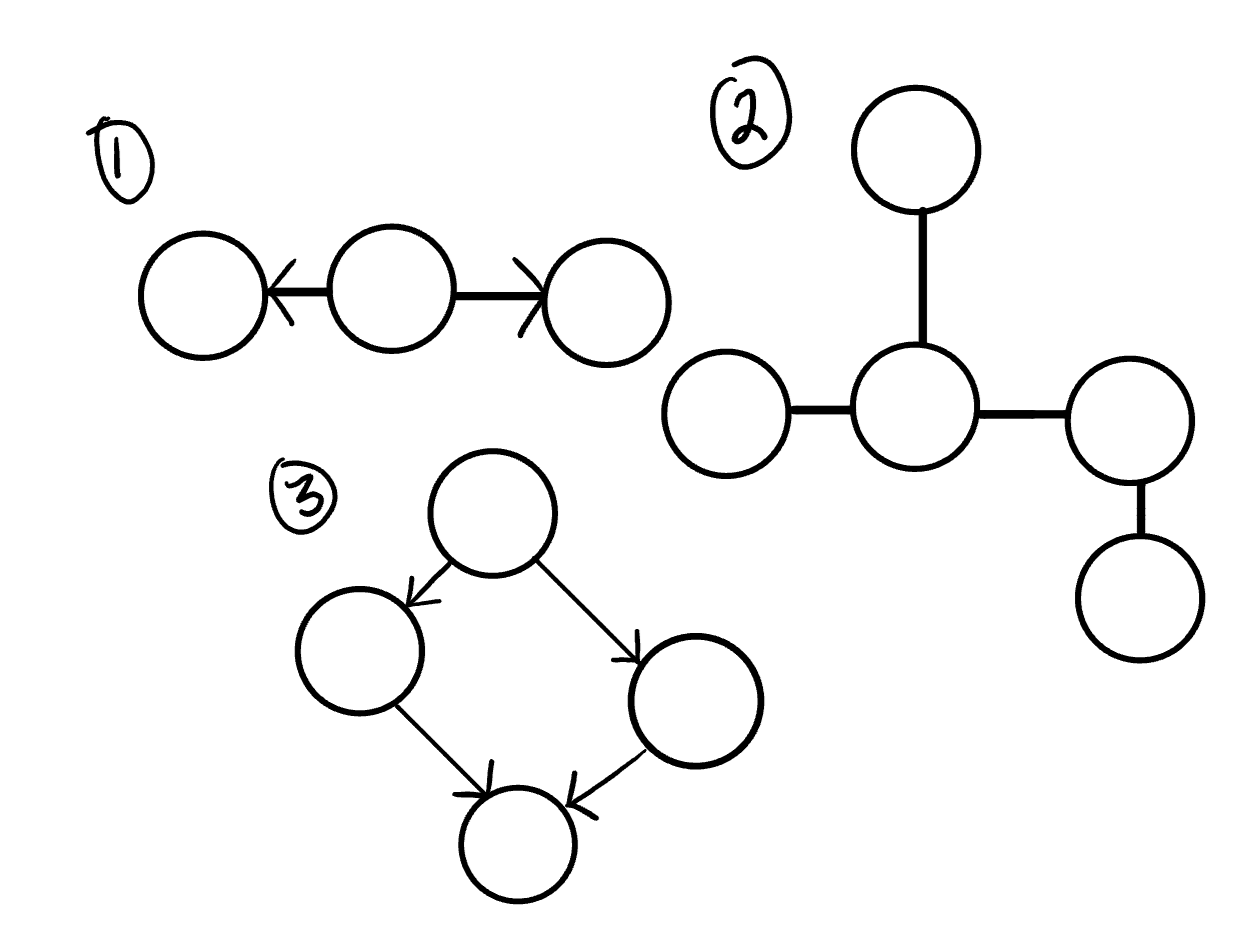
- A directed acyclic graph is also called a DAG. This can also be represented as what we know as a tree.
- Cyclic Graphs
- A Cyclic graph is a graph that has cycles.
- A cycle is defined as a path of a positive length that starts and ends at the same vertex.